Cryptanalysis
Cryptanalysis (from the Greek kryptós, "hidden", and analýein, "to loosen" or "to untie") is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key. In non-technical language, this is the practice of codebreaking or cracking the code, although these phrases also have a specialised technical meaning (see code).
Cryptanalysis is also used to refer to any attempt to circumvent the security of other types of cryptographic algorithms and protocols in general, and not just encryption. However, cryptanalysis usually excludes methods of attack that do not primarily target weaknesses in the actual cryptography, such as bribery, physical coercion, burglary, keystroke logging, and social engineering, although these types of attack are an important concern and are often more effective than traditional cryptanalysis.
Even though the goal has been the same, the methods and techniques of cryptanalysis have changed drastically through the history of cryptography, adapting to increasing cryptographic complexity, ranging from the pen-and-paper methods of the past, through machines like Bombes and Colossus computers at Bletchley Park in World War II, to the computer-based schemes of the present. The results of cryptanalysis have also changed — it is no longer possible to have unlimited success in codebreaking, and there is a hierarchical classification of what constitutes an attack. In the mid-1970s, a new class of cryptography was introduced: asymmetric cryptography. Methods for breaking these cryptosystems are typically radically different from before, and usually involve solving carefully constructed problems in pure mathematics, the best-known being integer factorization.
Contents |
History of cryptanalysis
Cryptanalysis has coevolved together with cryptography, and the contest can be traced through the history of cryptography—new ciphers being designed to replace old broken designs, and new cryptanalytic techniques invented to crack the improved schemes. In practice, they are viewed as two sides of the same coin: in order to create secure cryptography, you have to design against possible cryptanalysis.
Classical cryptanalysis
Although the actual word "cryptanalysis" is relatively recent (it was coined by William Friedman in 1920), methods for breaking codes and ciphers are much older. The first known recorded explanation of cryptanalysis was given by 9th-century Arabian polymath, Al-Kindi (also known as "Alkindus" in Europe), in A Manuscript on Deciphering Cryptographic Messages. This treatise includes a description of the method of frequency analysis (Ibrahim Al-Kadi, 1992- ref-3). Italian scholar Giambattista della Porta was author of a seminal work on cryptanalysis "De Furtivis Literarum Notis".[1]
Frequency analysis is the basic tool for breaking most classical ciphers. In natural languages, certain letters of the alphabet appear more frequently than others; in English, "E" is likely to be the most common letter in any sample of plaintext. Similarly, the digraph "TH" is the most likely pair of letters in English, and so on. Frequency analysis relies on a cipher failing to hide these statistics. For example, in a simple substitution cipher (where each letter is simply replaced with another), the most frequent letter in the ciphertext would be a likely candidate for "E". Frequency analysis of such a cipher is therefore relatively easy, provided that the ciphertext is long enough to give a reasonably representative count of the letters of the alphabet that it contains.[2]
In Europe during the 15th and 16th centuries, the idea of a polyalphabetic substitution cipher was developed, among others by the French diplomat Blaise de Vigenère (1523–96).[3] For some three centuries, the Vigenère cipher, which uses a repeating key to select different encryption alphabets in rotation, was considered to be completely secure (le chiffre indéchiffrable—"the indecipherable cipher"). Nevertheless, Charles Babbage (1791–1871) and later, independently, Friedrich Kasiski (1805–81) succeeded in breaking this cipher.[4] During World War I, inventors in several countries developed rotor cipher machines such as Arthur Scherbius' Enigma, in an attempt to minimise the repetition that had been exploited to break the Vigenère system.[5]
In practice, frequency analysis relies as much on linguistic knowledge as it does on statistics, but as ciphers became more complex, mathematics became more important in cryptanalysis. This change was particularly evident before and during World War II, where efforts to crack Axis ciphers required new levels of mathematical sophistication. Moreover, automation was first applied to cryptanalysis in that era with the Polish Bomba device, the British Bombe development of it, the use of punched card equipment, and in the Colossus computers — the first electronic digital computers to be controlled by a program.
Depth
Sending two or more messages with the same key is an insecure process. To a cryptanalyst the messages are then said to be "in depth".[6] This may be detected by the messages having the same indicator by which the sending operator informs the receiving operator about the key generator initial settings for the message.[7] In a symmetrical cipher, the same key that was applied to the plaintext to produce the ciphertext is applied to the ciphertext to recover the plaintext. A simple example of such a system is the Vernam cipher in which a long key is bit-for-bit combined with the plaintext or ciphertext using the "XOR" operator (symbolized by  ):
):
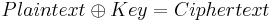 at each bit position
at each bit position
and
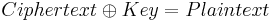 at each bit position
at each bit position
When the ciphertexts are in depth, combining them eliminates the common key, leaving just a combination of the two plaintexts:
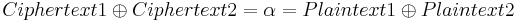 at each bit position
at each bit position
The individual plaintexts can then be worked out by trying probable words (or phrases) at various locations; when the corresponding section of  is XORed with a correct guess at the probable word, a stretch of the other plaintext is revealed, which can be recognized and (quite often) extended at each end, working back and forth between the plaintexts to recover much or all of them. When a recovered plaintext is then combined with its ciphertext, the key is revealed:
is XORed with a correct guess at the probable word, a stretch of the other plaintext is revealed, which can be recognized and (quite often) extended at each end, working back and forth between the plaintexts to recover much or all of them. When a recovered plaintext is then combined with its ciphertext, the key is revealed:
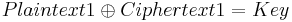 at each bit position
at each bit position
Knowledge of keys from a cipher may allow cryptanalysts to work out the system used for constructing them.
Depth reading can be applied in more complicated contexts to eliminate some of a system's parameters, or to "stack" messages so that source language statistics become exploitable. One way to properly align multiple messages that use the same periodic key starting at different positions is by the kappa test.
Modern cryptanalysis
Even though computation was used to great effect in cryptanalysis of the Enigma and other systems during World War II, it also made possible new methods of cryptography orders of magnitude more complex than ever before. Taken as a whole, modern cryptography has become much more impervious to cryptanalysis than the pen-and-paper systems of the past, and now seems to have the upper hand against pure cryptanalysis. The historian David Kahn notes,
"Many are the cryptosystems offered by the hundreds of commercial vendors today that cannot be broken by any known methods of cryptanalysis. Indeed, in such systems even a chosen plaintext attack, in which a selected plaintext is matched against its ciphertext, cannot yield the key that unlock[s] other messages. In a sense, then, cryptanalysis is dead. But that is not the end of the story. Cryptanalysis may be dead, but there is - to mix my metaphors - more than one way to skin a cat.".[8]
Kahn goes on to mention increased opportunities for interception, bugging, side channel attacks, and quantum computers as replacements for the traditional means of cryptanalysis. In 2010, former NSA technical director Brian Snow said that both academic and government cryptographers are "moving very slowly forward in a mature field."[9]
However, any postmortems for cryptanalysis may be premature. While the effectiveness of cryptanalytic methods employed by intelligence agencies remains unknown, many serious attacks against both academic and practical cryptographic primitives have been published in the modern era of computer cryptography:
- The block cipher Madryga, proposed in 1984 but not widely used, was found to be susceptible to ciphertext-only attacks in 1998.
- FEAL-4, proposed as a replacement for the DES standard encryption algorithm but not widely used, was demolished by a spate of attacks from the academic community, many of which are entirely practical.
- The A5/1, A5/2, CMEA, and DECT systems used in mobile and wireless phone technology can all be broken in hours, minutes or even in real-time using widely-available computing equipment.
- Brute-force keyspace search has broken some real-world ciphers and applications, including single-DES (see EFF DES cracker), 40-bit "export-strength" cryptography, and the DVD Content Scrambling System.
- In 2001, Wired Equivalent Privacy (WEP), a protocol used to secure Wi-Fi wireless networks, was shown to be breakable in practice because of a weakness in the RC4 cipher and aspects of the WEP design that made related-key attacks practical. WEP was later replaced by Wi-Fi Protected Access.
- In 2008, researchers conducted a proof-of-concept break of SSL using weaknesses in the MD5 hash function and certificate issuer practices that made it possible to exploit collision attacks on hash functions. The certificate issuers involved changed their practices to prevent the attack from being repeated.
Thus, while the best modern ciphers may be far more resistant to cryptanalysis than the Enigma, cryptanalysis and the broader field of information security remain quite active.
The results of cryptanalysis
Successful cryptanalysis has undoubtedly influenced history; the ability to read the presumed-secret thoughts and plans of others can be a decisive advantage. For example, in England in 1587, Mary, Queen of Scots was tried and executed for treason for her involvement in three plots to assassinate Elizabeth I of England which were known about because her coded correspondence with fellow conspirators had been deciphered by Thomas Phelippes; in World War I, the breaking of the Zimmermann Telegram was instrumental in bringing the United States into the war; in World War II, the cryptanalysis of the German ciphers — including the Enigma machine and the Lorenz cipher — has been credited with everything between shortening the end of the European war by a few months to determining the eventual result (see Ultra). The United States also benefited from the cryptanalysis of the Japanese Purple code (see Magic).
Governments have long recognized the potential benefits of cryptanalysis for intelligence, both military and diplomatic, and established dedicated organizations devoted to breaking the codes and ciphers of other nations, for example, GCHQ and the NSA, organizations which are still very active today. In 2004, it was reported that the United States had broken Iranian ciphers. (It is unknown, however, whether this was pure cryptanalysis, or whether other factors were involved:[10]).
Types of cryptanalytic attack
Cryptanalytic attacks vary in potency and how much of a threat they pose to real-world cryptosystems. A certificational weakness is a theoretical attack that is unlikely to be applicable in any real-world situation; the majority of results found in modern cryptanalytic research are of this type. Essentially, the practical importance of an attack is dependent on the answers to the following four questions:
- What knowledge and capabilities does the attacker need?
- How much additional secret information is deduced?
- How much computation is required? (What is the computational complexity?)
- Does the attack break the full cryptosystem, or only a weakened version?
Access needed for the attack
Cryptanalysis can be performed under a number of assumptions about how much access the attacker has to the system under attack. As a basic starting point it is normally assumed that, for the purposes of analysis, the general algorithm is known; this is Kerckhoffs' principle of "the enemy knows the system". This is a reasonable assumption in practice — throughout history, there are countless examples of secret algorithms falling into wider knowledge, variously through espionage, betrayal and reverse engineering. (On occasion, ciphers have been reconstructed through pure deduction; for example, the German Lorenz cipher and the Japanese Purple code, and a variety of classical schemes).
Other assumptions include:
- Ciphertext-only: the cryptanalyst has access only to a collection of ciphertexts or codetexts.
- Known-plaintext: the attacker has a set of ciphertexts to which he knows the corresponding plaintext.
- Chosen-plaintext (chosen-ciphertext): the attacker can obtain the ciphertexts (plaintexts) corresponding to an arbitrary set of plaintexts (ciphertexts) of his own choosing.
- Adaptive chosen-plaintext: like a chosen-plaintext attack, except the attacker can choose subsequent plaintexts based on information learned from previous encryptions. Similarly Adaptive chosen ciphertext attack.
- Related-key attack: Like a chosen-plaintext attack, except the attacker can obtain ciphertexts encrypted under two different keys. The keys are unknown, but the relationship between them is known; for example, two keys that differ in the one bit.
These types of attack clearly differ in how plausible they would be to mount in practice. Although some are more likely than others, cryptographers will often take a conservative approach to security and assume the worst-case when designing algorithms, reasoning that if a scheme is secure even against unrealistic threats, then it should also resist real-world cryptanalysis as well.
The assumptions are often more realistic than they might seem upon first glance. For a known-plaintext attack, the cryptanalyst might well know or be able to guess at a likely part of the plaintext, such as an encrypted letter beginning with "Dear Sir", or a computer session starting with "LOGIN:". A chosen-plaintext attack is less likely, but it is sometimes plausible: for example, you could convince someone to forward a message you have given them, but in encrypted form. Related-key attacks are mostly theoretical, although they can be realistic in certain situations, for example, when constructing cryptographic hash functions using a block cipher.
Usefulness of attack results
The results of cryptanalysis can also vary in usefulness. For example, cryptographer Lars Knudsen (1998) classified various types of attack on block ciphers according to the amount and quality of secret information that was discovered:
- Total break — the attacker deduces the secret key.
- Global deduction — the attacker discovers a functionally equivalent algorithm for encryption and decryption, but without learning the key.
- Instance (local) deduction — the attacker discovers additional plaintexts (or ciphertexts) not previously known.
- Information deduction — the attacker gains some Shannon information about plaintexts (or ciphertexts) not previously known.
- Distinguishing algorithm — the attacker can distinguish the cipher from a random permutation.
Similar considerations apply to attacks on other types of cryptographic algorithm.
Computational resources required
Attacks can also be characterised by the resources they require. Those resources include:
- Time — the number of computation steps (like encryptions) which must be performed.
- Memory — the amount of storage required to perform the attack.
- Data — the quantity of plaintexts and ciphertexts required.
It's sometimes difficult to predict these quantities precisely, especially when the attack isn't practical to actually implement for testing. But academic cryptanalysts tend to provide at least the estimated order of magnitude of their attacks' difficulty, saying, for example, "SHA-1 collisions now 252."[11]
Bruce Schneier notes that even computationally impractical attacks can be considered breaks: "Breaking a cipher simply means finding a weakness in the cipher that can be exploited with a complexity less than brute force. Never mind that brute-force might require 2128 encryptions; an attack requiring 2110 encryptions would be considered a break...simply put, a break can just be a certificational weakness: evidence that the cipher does not perform as advertised."[12]
Partial breaks
Academic attacks are often against weakened versions of a cryptosystem, such as a block cipher or hash function with some rounds removed. Many, but not all, attacks become exponentially more difficult to execute as rounds are added to a cryptosystem,[13] so it's possible for the full cryptosystem to be strong even though reduced-round variants are weak. Nonetheless, partial breaks that come close to breaking the original cryptosystem may mean that a full break will follow; the successful attacks on DES, MD5, and SHA-1 were all preceded by attacks on weakened versions.
Academic weakness versus practical weakness
In academic cryptography, a weakness or a break in a scheme is usually defined quite conservatively: it might require impractical amounts of time, memory, or known plaintexts. It also might require the attacker be able to do things many real-world attackers can't: for example, the attacker may need to choose particular plaintexts to be encrypted or even to ask for plaintexts to be encrypted using several keys related to the secret key. Furthermore, it might only reveal a small amount of information, enough to prove the cryptosystem imperfect but too little to be useful to real-world attackers. Finally, an attack might only apply to a weakened version of cryptographic tools, like a reduced-round block cipher, as a step towards breaking of the full system.[12]
Cryptanalysis of asymmetric cryptography
Asymmetric cryptography (or public key cryptography) is cryptography that relies on using two keys; one private, and one public. Such ciphers invariably rely on "hard" mathematical problems as the basis of their security, so an obvious point of attack is to develop methods for solving the problem. The security of two-key cryptography depends on mathematical questions in a way that single-key cryptography generally does not, and conversely links cryptanalysis to wider mathematical research in a new way.
Asymmetric schemes are designed around the (conjectured) difficulty of solving various mathematical problems. If an improved algorithm can be found to solve the problem, then the system is weakened. For example, the security of the Diffie-Hellman key exchange scheme depends on the difficulty of calculating the discrete logarithm. In 1983, Don Coppersmith found a faster way to find discrete logarithms (in certain groups), and thereby requiring cryptographers to use larger groups (or different types of groups). RSA's security depends (in part) upon the difficulty of integer factorization — a breakthrough in factoring would impact the security of RSA.
In 1980, one could factor a difficult 50-digit number at an expense of 1012 elementary computer operations. By 1984 the state of the art in factoring algorithms had advanced to a point where a 75-digit number could be factored in 1012 operations. Advances in computing technology also meant that the operations could be performed much faster, too. Moore's law predicts that computer speeds will continue to increase. Factoring techniques may continue to do so as well, but will most likely depend on mathematical insight and creativity, neither of which has ever been successfully predictable. 150-digit numbers of the kind once used in RSA have been factored. The effort was greater than above, but was not unreasonable on fast modern computers. By the start of the 21st century, 150-digit numbers were no longer considered a large enough key size for RSA. Numbers with several hundred digits were still considered too hard to factor in 2005, though methods will probably continue to improve over time, requiring key size to keep pace or other methods such as elliptic curve cryptography to be used.
Another distinguishing feature of asymmetric schemes is that, unlike attacks on symmetric cryptosystems, any cryptanalysis has the opportunity to make use of knowledge gained from the public key.
Quantum computing applications for cryptanalysis
Quantum computers, which are still in the early phases of research, have potential use in cryptanalysis. For example, Shor's Algorithm could factor large numbers in polynomial time, in effect breaking some commonly used forms of public-key encryption.
By using Grover's algorithm on a quantum computer, brute-force key search can be made quadratically faster. However, this could be countered by doubling the key length.
Methods of cryptanalysis
Classical cryptanalysis:
Symmetric algorithms:
- Boomerang attack
- Brute force attack
- Davies' attack
- Differential cryptanalysis
- Impossible differential cryptanalysis
- Improbable differential cryptanalysis
- Integral cryptanalysis
- Linear cryptanalysis
- Meet-in-the-middle attack
- Mod-n cryptanalysis
- Related-key attack
- Sandwich attack
- Slide attack
- XSL attack
Hash functions:
Network attacks:
External attacks:
See also
Related topics
- Information security, the overarching goal of most cryptography
- Security vulnerability; vulnerabilities can include cryptographic or other flaws
- Security engineering, the design of applications and protocols
- Information assurance, a term for information security often used in government
- Economics of security
General
- Cryptanalysis of the Enigma
- Cryptography
- Cryptography portal
- Decipherment
- Topics in cryptography
- National Cipher Challenge
- Zendian Problem
Historic cryptanalysts
- Conel Hugh O'Donel Alexander
- Charles Babbage
- Lambros D. Callimahos
- Alastair Denniston
- Agnes Meyer Driscoll
- Elizebeth Friedman
- William F. Friedman, the father of modern cryptology
- Meredith Gardner
- Friedrich Kasiski
- Al-Kindi
- Dilly Knox
- Solomon Kullback
- Marian Rejewski
- Joseph Rochefort, whose contributions affected the outcome of the Battle of Midway
- Frank Rowlett
- Abraham Sinkov
- Giovanni Soro, the Renaissance's first outstanding cryptanalyst
- John Tiltman
- Alan Turing
- Herbert Yardley
Notes
- ^ Crypto History
- ^ Singh 1999, p. 17
- ^ Singh 1999, pp. 45–51
- ^ Singh 1999, pp. 63–78
- ^ Singh 1999, p. 116
- ^ Churchhouse 2002, p. 34
- ^ Churchhouse 2002, pp. 33, 86
- ^ David Kahn Remarks on the 50th Anniversary of the National Security Agency, November 1, 2002.
- ^ Tim Greene, Network World, Former NSA tech chief: I don't trust the cloud. Retrieved March 14, 2010.
- ^ "Breaking codes: An impossible task?". BBC News. June 21, 2004. http://news.bbc.co.uk/1/hi/technology/3804895.stm.
- ^ [1]
- ^ a b Schneier 2000
- ^ For an example of an attack that cannot be prevented by additional rounds, see slide attack.
References
- Ibrahim A. Al-Kadi,"The origins of cryptology: The Arab contributions”, Cryptologia, 16(2) (April 1992) pp. 97–126.
- Friedrich L. Bauer: "Decrypted Secrets". Springer 2002. ISBN 3-540-42674-4
- Churchhouse, Robert (2002). Codes and Ciphers: Julius Caesar, the Enigma and the Internet. Cambridge: Cambridge University Press. ISBN 978-0-521-00890-7
- Helen Fouché Gaines, "Cryptanalysis", 1939, Dover. ISBN 0-486-20097-3
- David Kahn, "The Codebreakers - The Story of Secret Writing", 1967. ISBN 0-684-83130-9
- Lars R. Knudsen: Contemporary Block Ciphers. Lectures on Data Security 1998: 105-126
- Schneier, Bruce (January 2000). "A Self-Study Course in Block-Cipher Cryptanalysis". Cryptologia 24 (1): 18–34. doi:10.1080/0161-110091888754. https://www.schneier.com/paper-self-study.html
- Abraham Sinkov, Elementary Cryptanalysis: A Mathematical Approach, Mathematical Association of America, 1966. ISBN 0-88385-622-0
- Christopher Swenson, Modern Cryptanalysis: Techniques for Advanced Code Breaking, ISBN 978-0470135938
- Friedman, William F., Military Cryptanalysis, Part I, ISBN 0-89412-044-1
- Friedman, William F., Military Cryptanalysis, Part II, ISBN 0-89412-064-6
- Friedman, William F., Military Cryptanalysis, Part III, Simpler Varieties of Aperiodic Substitution Systems, ISBN 0-89412-196-0
- Friedman, William F., Military Cryptanalysis, Part IV, Transposition and Fractionating Systems, ISBN 0-89412-198-7
- Friedman, William F. and Lambros D. Callimahos, Military Cryptanalytics, Part I, Volume 1, ISBN 0-89412-073-5
- Friedman, William F. and Lambros D. Callimahos, Military Cryptanalytics, Part I, Volume 2, ISBN 0-89412-074-3
- Friedman, William F. and Lambros D. Callimahos, Military Cryptanalytics, Part II, Volume 1, ISBN 0-89412-075-1
- Friedman, William F. and Lambros D. Callimahos, Military Cryptanalytics, Part II, Volume 2, ISBN 0-89412-076-X
- Singh, Simon (1999). The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography. London: Fourth Estate. pp. 143–189. ISBN 1-85702-879-1.
External links
- Basic Cryptanalysis (files contain 5 line header, that has to be removed first)
- Distributed Computing Projects
- Simon Singh's crypto corner
- The National Museum of Computing
- UltraAnvil tool for attacking simple substitution ciphers
|
||||||||||